曲线积分与曲面积分

一、选择题

设函数Q（x，y）＝x/y2，如果对上半平面（y＞0）内的任意有向光滑封闭

曲线C都有

那么函数P（x，y）可取为（）。[数一2019研]

A．y－x2/y3

B．1/y－x2/y3

C．1/x－1/y

D．x－1/y

【答案】D

【解析】由题意可知，y＞0时积分与路径无关，因而Q/x＝P/y＝1/y2，排除选项A和B。虽然C选项满足上述条件，但其在y轴正半轴无意义，故选D。

二、填空题

1设L为球面x2＋y2＋z2＝1与平面x＋y＋z＝0的交线，求 ____。[数一2018研]

【答案】－π/3

【解析】由L的方程可看出，曲线L对于x，y，z具有轮换对称性。因此

又由于xy＋yz＋xz＝[（x＋y＋z）2－（x2＋y2＋z2）]/2。因此

由于L是以球心为圆心，且半径等于球半径的一个圆，故 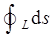的周长L＝2π，所以原积分＝－（1/6）×2π＝－π/3。

2若曲线积分 在区域D＝{（x，y）|x2＋y2＜1}内与路径无关，则a＝______。[数一2017研]

【答案】－1

【解析】P（x，y）＝x/（x2＋y2－1），Q（x，y）＝－ay/（x2＋y2－1），曲线积分与路径无关等价于P/y＝Q/x。又P/y＝－2xy/（x2＋y2－1）2，Q/x＝2axy/（x2＋y2－1）2，计算得a＝－1。

三、解答题

1计算曲线积分，其中L是x2＋y2＝2，方向为逆时针方向。

[数一2020研]

解：设P＝（4x－y）/（4×2＋y2），Q＝（x＋y）/（4×2＋y2），

则

取路径Lε：4×2＋y2＝ε2，方向为顺时针方向，Dε为Lε所围曲面，

则